Octaves and scale formation

Octaves

When you play an ocarina the air entering and leaving the chamber pushes on the air in your environment. This causes waves to travel through the air much like those on the surface of a pond. When they reach your ears you hear a sound.

These waves can be visualised as a graph. High points represent pressure fronts and the low points represent the low pressure regions between them.

All waves have a frequency, the number of peaks or troughs that pass a point in space in 1 second. When two notes sound and one is exactly double the frequency of the other the human mind perceives both with the same tone. This is called an octave. Incidentally the phenomenon is not limited to a single doubling. If the high wave is again doubled, now 4 times the frequency of the first, all 3 are perceived equivalently.

Because of this the notes used in music repeat. This repetition exists on all instruments but is most obvious on the piano keyboard. Western music divides the octave into 12 notes, 12 sequential white and black keys. After note 12, it returns to note 1 an octave higher or double the frequency.

The keyboard simply repeats these same 12 notes from left to right. This grouping can be identified easily by looking at the black keys, which are grouped into twos and threes.

If you pick any key within one octave and play a tune, then play the same sequence from that key in a different octave it will sound like the same tune. You can also play a sequence in two or more octaves at the same time. When a note sounds in multiple octaves the highest is heard as the melody and the lower ones create a richer tone.

Timbre

As the frequency of a sound is determined only by its peaks the shape of the wave in between can vary. These differences are perceived as tone colour, or timbre.

Timbre is what makes an ocarina sound like an ocarina, a violin sound like a violin, and a piano sound like a piano. Sounds can have the same pitch, but have a different timbre.

You can hear the same pitch played on a collection of instruments with different timbres in the following audio sample:

How to form a Major scale

Try using the editor below to make a melody using all 12 notes. The vertical position corresponds to the 12 different notes. You can place notes by clicking on the grid, and move them by dragging them.

Have a play, and observe how it sounds:

What you may notice is that music formed from all of these notes sounds very 'ghostly' and ungrounded. It is very difficult to tell one note from another.

The reason is that the distance between any two of these adjacent notes is called a 'half step' or 'semitone', and all semitones sound the same. Note 1 to note 2 is a half step, Note 2 to note 3 is also a half step and so on.

Note that the 12 notes are being displayed in a line as it makes things easier to visualise. These correlate with the 12 keys numbered in the previous diagram of the piano keyboard.

This 12 note scale is called the 'chromatic scale', and it is rarely used as a whole. Rather, music is built by selecting a subset of these notes that sound good together.

Most western music is tonal, it is written to highlight a single note as it's focal point. This cannot be achieved using a scale comprised of just half steps. To solve this problem another interval is used: the whole step, which is simply two half steps in sequence. Here are a few whole steps:

By using a mixture of these two intervals scales can be built. Among the most commonly used in music is the major scale which is defined as the following pattern. Notice that this pattern is asymmetrical. This gives each of the notes a unique sound and gives the ear a hook so that it can tell where it is.

Whole, Whole, Half, Whole, Whole, Whole, Half

Using this single pattern you can form a major scale starting on note 1 as follows:

• Instruction 1 is a whole step, so you move forward to 3.
• Instruction 2 is a also a whole step, so you move to 5.
• Instruction 3 is a half step so you move forward from 5 to 6.

If you keep following the pattern you end up with: 1,3,5,6,8,10,12,1.

The layout of many instruments is based on this pattern, including the ocarina. It is actually visible in the sizes of the finger holes.

Actually, you can form a major scale by following the same pattern starting from any of the 12 chromatic notes. Thus, there are 12 major scales or 'keys'. These all sound remarkably similar, but are higher or lower in pitch.

The following tool allows you to scroll between all 12 patterns.

Naming the notes

As most music uses only 7 of the chromatic notes at a time It would be cumbersome to have to think about the additional 5 notes which you are not using. For example having to remember that the next note after 1 is 3, but that 6 follows 5 directly.

The standard note names are designed to hide these irregularities. The notes of the major scale starting from note 1 are named using the first seven letters of the alphabet. Note 1 is called C, followed by D, E, F, G, A, B and finally C an octave higher.

These are called the 'natural' notes, and the naming makes it is obvious that the note E follows D and F follows E despite the irregular spacing.

The other notes are called accidentals. They are named relatively using sharps (♯) or flats (♭). For now I'm only going to demonstrate sharps. Sharpening a note adds one semitone to it, 'C♯' is the note one semitone above C.

As it is the base of the system the scale of C Major needs no accidentals. If you form a scale from any other note they will be included. For example if you start on D you have two sharps, F♯ and C♯.

Musicians normally consider only the notes of the scale that they are using, and ignore all of the others. You can see how this looks for yourself in the following example if you change 'scale' between 'chromatic' and 'C major', notice how the gaps vanish.

Octave registers

• The note C1 is C in octave register 1 and the highest note in this register is B1.
• After this the next note is C2.
• Subsequent octaves are numbered sequentially.

In total 7 full octaves are commonly used in music. C8 exists by itself at the top. In the following audio example you may hear the note C played in all 8 octaves.

Any single chambered ocarina can only access a small portion of this range. For example an alto C ocarina plays from C5 to F6. See 'Ocarina keys and pitch ranges' for more details.

Enharmonic notes

The system defined before is a convenient way to think about the notes of music but it does have a problem. In the tool below the numbers have been replaced with letters and sharps. Have a play and see if you can spot what's wrong:

In some cases there are repeat letters for example F Major, if this scale is noted using sharps you get: F, G, A, A♯, C, D, E, F. The letter 'A' shows up twice while B is missing altogether. It is conventional to use each letter only once for clarity.

This problem can be solved by using flats (♭) instead of sharps. Adding a flat to a note lowers it by one semitone. For example if you begin from the note B and add a flat, you descend to the chromatic note between A and B.

Using flats the scale of F major can be written cleanly:

F, G, A, B♭, C, D, E, F

Because of this the chromatic notes actually have two names, one raising the note below and one lowering the note above, i.e. C♯ and D♭. These are called enharmonic, a music term that means two names for the same thing.

In some cases the natural notes can also be enharmonic. For example here is C♯ major as displayed by the above tool:

C♯, D♯, F, F♯, G♯, A♯, C, C♯

The names F and C appear twice, while E and B are not used at all. In this case it is better to call F, 'E♯' and C, 'B♯'. Now every letter is used once:

C♯, D♯, E♯, F♯, G♯, A♯, B♯, C♯

Here are the notes of the 12 Major scales how their notes are commonly named. There is no need to memorise these, as you can look them up when you need them:

• C - C, D, E, F, G, A, B, C
• C♯ - C♯, D♯, E♯, F♯, G♯, A♯, B♯, C♯
• D - D, E, F♯, G, A, B, C♯, D
• E♭ - E♭, F, G, A♭, B♭, C, D, E♭
• E - E, F♯, G♯, A, B, C♯, D♯, E
• F - F, G, A, B♭, C, D, E, F
• F♯ - F♯, G♯, A♯, B, C♯, D♯, E♯, F♯
• G - G, A, B, C, D, E, F♯, G
• A♭ - A♭, B♭, C, D♭, E♭, F, G, A♭
• A - A, B, C♯, D, E, F♯, G♯, A
• B♭ - B♭, C, D, E♭, F, G, A, B♭
• B - B, C♯, D♯, E, F♯, G♯, A♯, B

Although note that they are more commonly organised in the order of increasing sharps / flats, following the circle of fifths:

Transposition

Transposition refers to the ability to raise or lower the pitch of a melody, and it will sound like the same melody despite the change in pitch. It is possible as all of the notes within the chromatic scale are a semitone apart.

You can see and hear this for yourself using the tool below. The 'transposition' slider moves the notes, and press play to hear how it sounds.

Another way of thinking about this is to realise that if two scales are based on the same pattern, they are equivalent. You can thus take the notes of both scales, and number them starting from the tonic. C and D major for example:

C major scale degrees

D major scale degrees

You can then substitute the note of one scale with the equivalent note of the other one. For example the notes 'E, C, D' in C major have the numbers '3, 1, 2'. So you substitute them for ' F♯, E, D'.

The value of transposition

The ability to transpose music is very useful for limited range instruments like the ocarina. It means that you can alter melodies that would be impossible to play, and make them fit within the range of your instrument.

Transposing also allows you to create variation in a performance. If music remains in the same key for a long time it can sound monotonous.

Transposition as a concept is extremely simple as you can see, but the nature of instrument fingering systems, and other things like music notation can make it look much more complicated than it is.

Closing notes, and other scales

Have a play around with these concepts and they should start to feel natural pretty quickly, it starts to make sense once you put it into practice.

Understanding octaves and scale formation is of great help in playing the ocarina, as they have such a limited range. It lets you understand how the different pitch ranges of ocarinas relate to each other, and the music you want to play on them.

In particular, transposition, and choosing ocarinas to provide the range of notes that you need are critical skills for real world playing.

Once you start to understand the basics of how scales are formed, a few questions may arise. For instance, what would happen if you formed a scale by following a different pattern? The answer is that you get a different type of scale.

Quite a few different scales exist, including the major, minor, and blues scales which you can hear below:

For example the natural minor scale is built from the pattern:

Whole, Half, Whole, Whole, Half, Whole, Whole

Another question that you may have is why the naming of the notes in the major scale starts from C instead of A. This also relates to the minor scale.

The pattern that the minor scale is formed from is actually the same as the major scale, just rotated by a few steps. You take 'Whole, Half' from the end of the major scale formula and put it at the start.

Thus A minor and C major share the same notes, and differ only in the tonic note. The naming is convenient as it creates a clear relationship between the two scales:

A minor:

A, B, C, D, E, F, G, A

C Major:

C, D, E, F, G, A, B, C

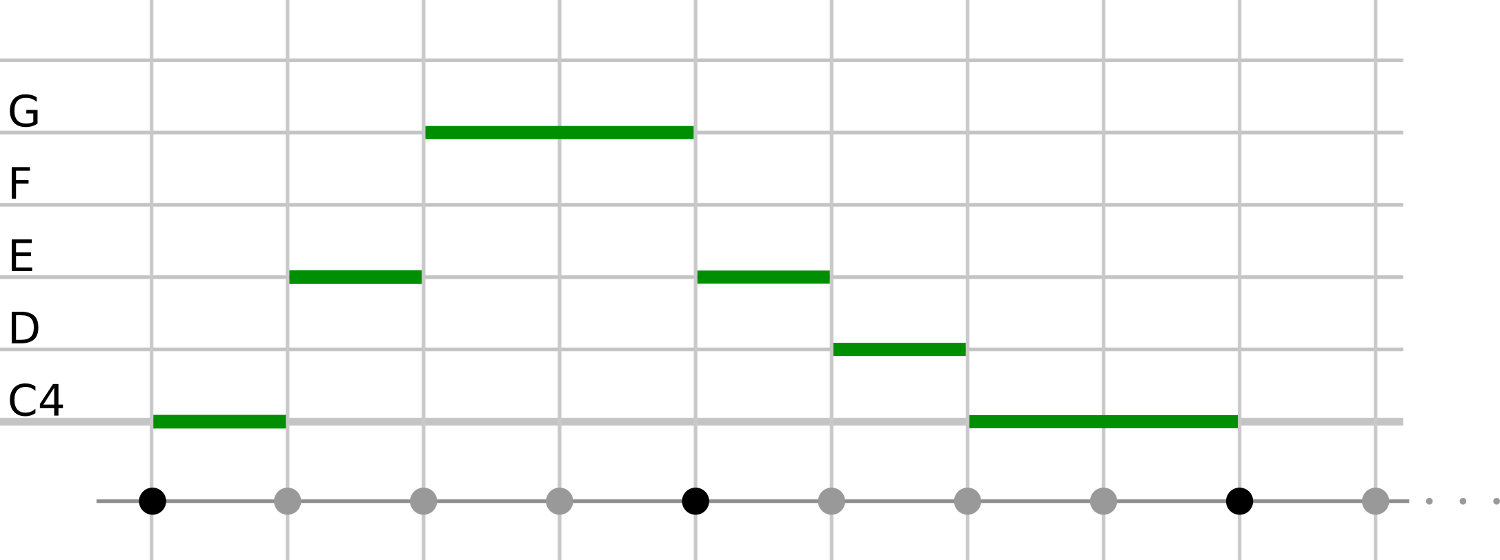
If you want to take this same concept further, it would be worth looking up the 'modes' of the major scale. Essentially you can form a unique scale from all 7 of the notes.